보스턴 집 값 예측하기!!
from pandas import read_csv
url = 'https://raw.githubusercontent.com/PinkWink/forML_study_data/refs/heads/main/data/boston_housing.csv'
column_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'PRICE']
boston_pd = read_csv(url, delimiter=r'\s+', names=column_names)
boston_pdurl을 통해 csv파일을 pandas를 통해 DataFrame으로 만들어 주는 작업을 하였습니다.

1. 우선 histogram을 통해 가격이 어떻게 분포하고 있는지 확인 해보겠습니다.
import plotly.express as px
fig = px.histogram(boston_pd, x='PRICE')
fig.show()
그래프를 보아하니 분포의 상태가 오른쪽 꼬리가 긴 모양 형태를 보아서는 비싼 집들이 어느 정도 분포하는 것으로 보입니다.
2. 이번에는 상관 계수를 통해 가격에 영향을 주는 컬럼이 어떤 것이 있는지 확인 해보겠습니다.
import matplotlib.pyplot as plt
import seaborn as sns
corr_mat = boston_pd.corr().round(1) # 상관계수 구하기
sns.heatmap(data=corr_mat, annot=True, cmap='bwr'); # 구한 상관계수를 heatmap으로 표현
상관계수를 시각적으로 확인할 때 자주 사용하는 heatmap 그래프입니다.
맨 아래의 값들을 보니 PRICE에 영향을 많이 주는 컬럼은 RM(주택당 방 수)와 LSTAT(하위 계층 비율)인 것으로 확인이 되었습니다.
3. 이제 두 컬럼을 통해 가격이 어떻게 변동되는지 확인해 보겠습니다.
sns.set_style('darkgrid')
fig, ax = plt.subplots(ncols=2)
sns.regplot(x='RM', y='PRICE', data=boston_pd, ax=ax[0])
sns.regplot(x='LSTAT', y='PRICE', data=boston_pd, ax=ax[1])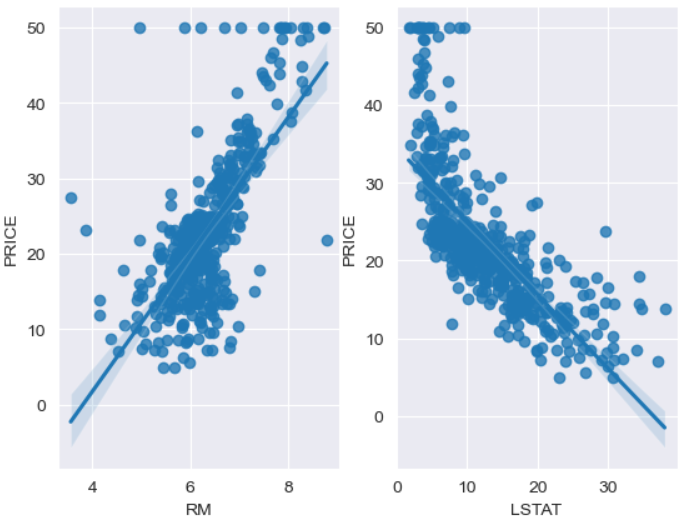
그래프를 보아하니 주택에 방 수가 많아질수록 가격이 올라가는 것이 확인 되고
두번째로 하위 계층 비율이 높을수록(하위 계층 사는 사람이 많을수록) 가격이 떨어지는 것이 확인 됩니다. 제 생각에는 하위 계층이 많이 사는 지역은 가격이 낮을 것 같습니다.
4. 이제 모든 컬럼들(특성은 price를 뺀 나머지 = 다중 특성!!)을 이용하여 선형 회귀를 통해 가격을 예측해보는 코드를 짜보겠습니다.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 특성(feature) 값만 X에 넣어줍니다.
X = boston_pd.drop('PRICE', axis=1)
# 정답(Label)값을 y에 넣어줍니다.
y= boston_pd['PRICE']
# 훈련 세트와 테스트 세트를 8:2 비율로 나눠줍니다.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)
# 선형회귀 모델링을 이용하여 학습시킵니다.
reg = LinearRegression()
reg.fit(X_train, y_train)위의 코드 처럼 데이터를 훈련세트와 테스트 세트로 나눠준 후 선형회귀 모델을 통해 학습을 시켜줍니다.
5. 이번에는 RMSE (Root Mean Squared Error, 평균 제곱근 오차)를 사용하여 모델의 예측 오차를 계산 해보겠습니다.
import numpy as np
from sklearn.metrics import mean_squared_error
pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))
rmse_tr, rmse_test확인 해보니 훈련 세트와 테스트 세트의 오차는 (4.642806069019824, 4.931352584146702) 이정도 숫자가 나온 걸 봐서는 그렇게 큰 오차를 내는 것 같지는 않습니다.
6. 이번에는 모델링 된 것을 통해 그래프를 확인 해보겠습니다.
plt.scatter(y_test, pred_test)
plt.plot([0, 50], [0, 50], 'r')
보아하니 위로 올라갈 수록 값이랑 많이 벗어나는 것 같습니다. 제가 보기에는 해당 그래프는 오류가 많아 보입니다.
7. 이번에는 상관계수에서 가격에 영향을 주는 컬럼을 빼고 훈련을 시켜보겠습니다.
from sklearn.model_selection import train_test_split
# LSTAT 없이 측정하기
X = boston_pd.drop(['PRICE', 'LSTAT'], axis=1)
y= boston_pd['PRICE']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)
reg = LinearRegression()
reg.fit(X_train, y_train)
# 오차 계산
pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))
rmse_tr, rmse_test측정 값이 이렇게 나온 것으로 보아 (5.165137874244864, 5.295595032597148) 확실히 중요한 변수가 제외 되어 계산을 해보니 모델이 적합하지 않아 증가한 것으로 확인 되었습니다.
8. 의사결정 나무 회귀 모델을 사용해 주택 가격을 예측하고 RMSE를 계산해보겠습니다. 해당 모델은 훨씬 정확한 값을 도출해낼 수 있습니다.
from sklearn.tree import DecisionTreeRegressor
reg_dt = DecisionTreeRegressor(max_depth=2, random_state=13) # 깊이를 2로 하여 단순한 나무 사용
reg_dt.fit(X_train, y_train)
y_pred_dt = reg_dt.predict(X_test)
rmse_test = np.sqrt(mean_squared_error(y_test, y_pred_dt))
rmse_test해당 모델을 통해 학습한 뒤 RMSE를 측정해본 결과 위에서 나온 값과 크게 변함이 없는 값 (5.698005991702834)이 나온 것을 보아 하이퍼파라미터 조정이 더 필요하거나 더 많은 시도를 해야 될 것 같습니다.
이렇게 선형회귀를 통한 주택 값 예측을 해보았지만 확실히 선형 회귀를 통해서는 알아낼 수 있는 정보가 많지는 않은 것 같습니다. 제 생각에는 위에서의 그래프도 직선이 아닌 곡선 형태가 더 맞는 그래프였었던 거 같습니다.
다음에는 와인 가격을 예측하는 모델을 만들어 보겠습니다. 이상입니다.
이 글은 제로베이스 데이터 분석 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.
'Data Analyst > ML' 카테고리의 다른 글
| [Zero-base] Scaling & 분류 모델 평가 (1) | 2024.10.03 |
|---|---|
| [Zero-base] Linear Regression(Wine 구별, Scaler) (0) | 2024.10.01 |
| [Zero-base]Linear Regression (0) | 2024.09.30 |
| [Zero-Base] Machine Learning - 1 (0) | 2024.09.27 |
| ML - Matplotlib SubPlots (1) | 2024.09.16 |