Sample variaton(S^2) : 분산
우선 위의 이름과 같이 샘플에서의 분산에 대한 설명입니다.
데이터가 평균을 중심으로 얼마나 퍼져 있는지를 나타내는 통계적 지표입니다.
즉, 각 데이터 포인트가 평균값에서 얼마나 떨어져 있는지의 평균을 계산한 값입니다.
Sample Standard Deviation : 표준편차
표준편차는 평균값에 대해서 얼마나 떨어져 있는지에 대한 정도를 평균화 한 것입니다. 위의 분산의 설명과 같습니다.
하지만 표준 편차와 분산의 차이점은 명확합니다.
차이점
분산 : 제곱된 거리의 평균입니다.
표준 편차 : 분산에 루트를 씌워 원래 데이터와 동일한 단위를 가지도록 만든 값입니다.

위의 그림에서의 공식은 표준편차의 공식입니다. 여기서 제가 써놓은 것을 설명해보겠습니다.
우선 키를 통해 예시를 들어보겠습니다.
샘플링을 한 데이터에서의 키 들이 많이 수집이 됬습니다. 여기서 평균을 구한결과 171cm로 측정되었습니다. 그럼 이제 분산을 구해보았습니다. 분산은 루트를 씌우지않고 제곱을 합니다. 그럼 키의 단위인 cm는 사용할 수 없게됩니다...
이 때 처음 데이터의 단위인 cm를 맞추기 위해서 루트를 사용(표준 편차)하는 것입니다.
그리고 정규분포표에서 분산을 사용하지 않고 표준편차를 사용하는 이유이기도 합니다!!
중심 극한 정리
우선 저희는 Population의 분포 모습을 알 수 없습니다.(온 세상의 모든 데이터를 가지고 있지 않기 때문!!)
그렇다면, 어떻게 Population을 구할 수 있을까?
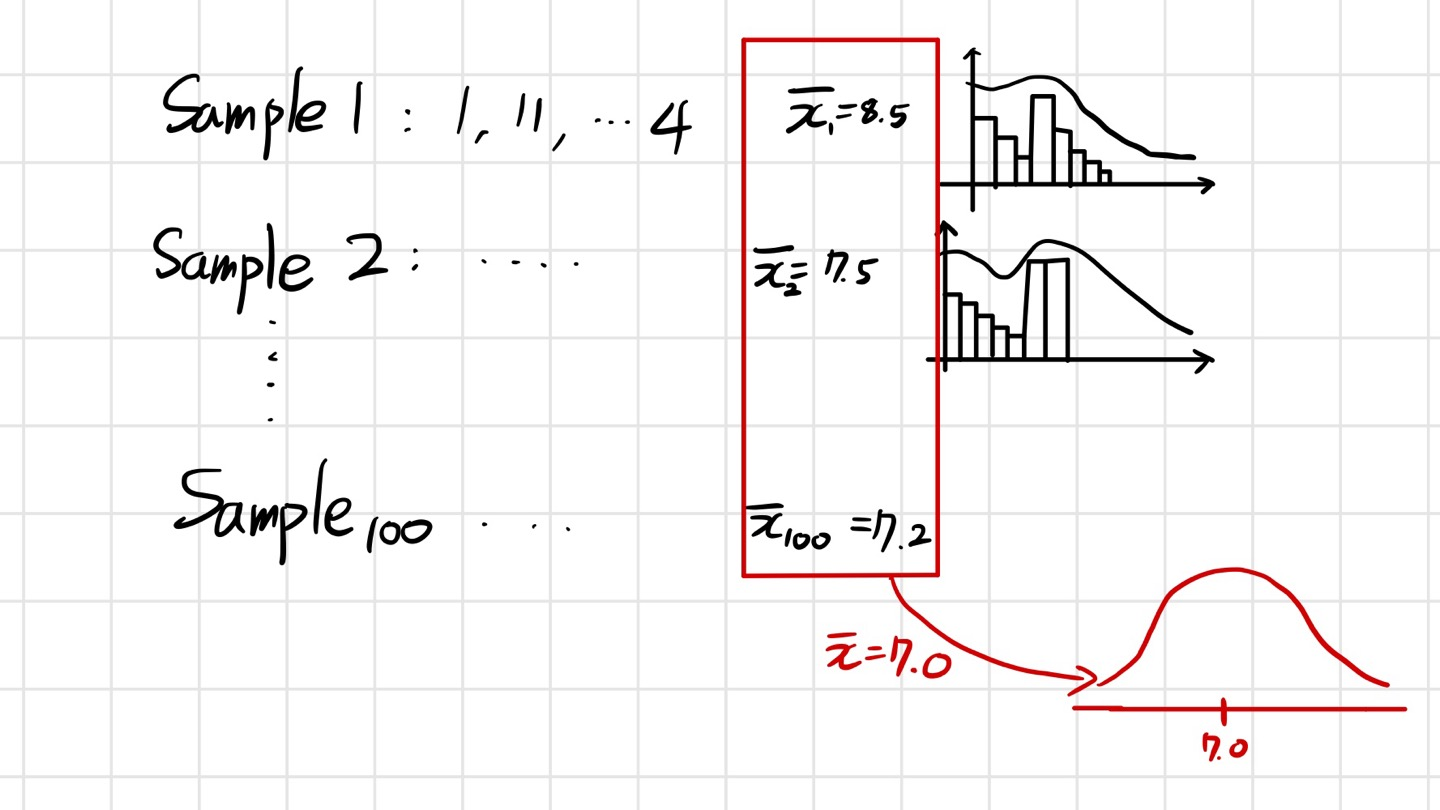
그 방법은 위의 그림과 같이 많은 샘플들의 통계치를 얻은 값을 통해 다시 분포를 그리면 해당 분포의 모습은 정규분포 모습을 가지게 됩니다.
-> 이 것을 중심극한정리라고 합니다.
즉, 샘플링 하는 횟수가 많아지면 통계치의 평균값을 Population(모집단)의 평균과 비슷해집니다.
(비슷하다 예측할 뿐 Population 분포와 같은 것은 아닙니다!)
해당 내용은 Data Scientist 이지영님의 영상을 보고 공부한 내용입니다.
이상입니다.
'Data Analyst > 기초 통계' 카테고리의 다른 글
| [기초 통계] 표본 분포 이해하기 (0) | 2024.10.28 |
|---|---|
| [기초 통계] 정규분포, 비대칭도, 첨도 (0) | 2024.10.23 |
| [기초 통계] Positive & Negative Skew(Mean vs Median) (1) | 2024.10.21 |
| [기초 통계] 이산 데이터 VS 연속성 데이터 (2) | 2024.10.16 |
| [기초 통계] p-value(유의 확률) (1) | 2024.10.16 |