1. 모집단(Population)
연구대상이라고도 한다. 하지만 모집단은 우리가 알아낼 수 없습니다.
SRS(Simple Random Sampling) : 모집단 전체를 조사할 수 없기 때문에 사용합니다.
2. 표본(Sample)
모집단을 알아낼 수 없기에 모집단과 비슷한 집단의 데이터들을 뽑아낸 것을 우리는 표본이라합니다.
표본에서 알아낸 통계치를 x_bar(표본 평균), S(표본 표준편차) 이용하여 모수를 추정합니다.
모수: 모집단에서 얻을 수 있는 평균(u)과 표준편차(seta) 등의 통계치를 말합니다.
3. 표본 분포
표본을 뽑으면 그 값이 모집단의 모수와 얼마나 가까운지 모르기에 여러번의 sampling을 통해 각각의 통계치를 분포로 나타낸 것이다.
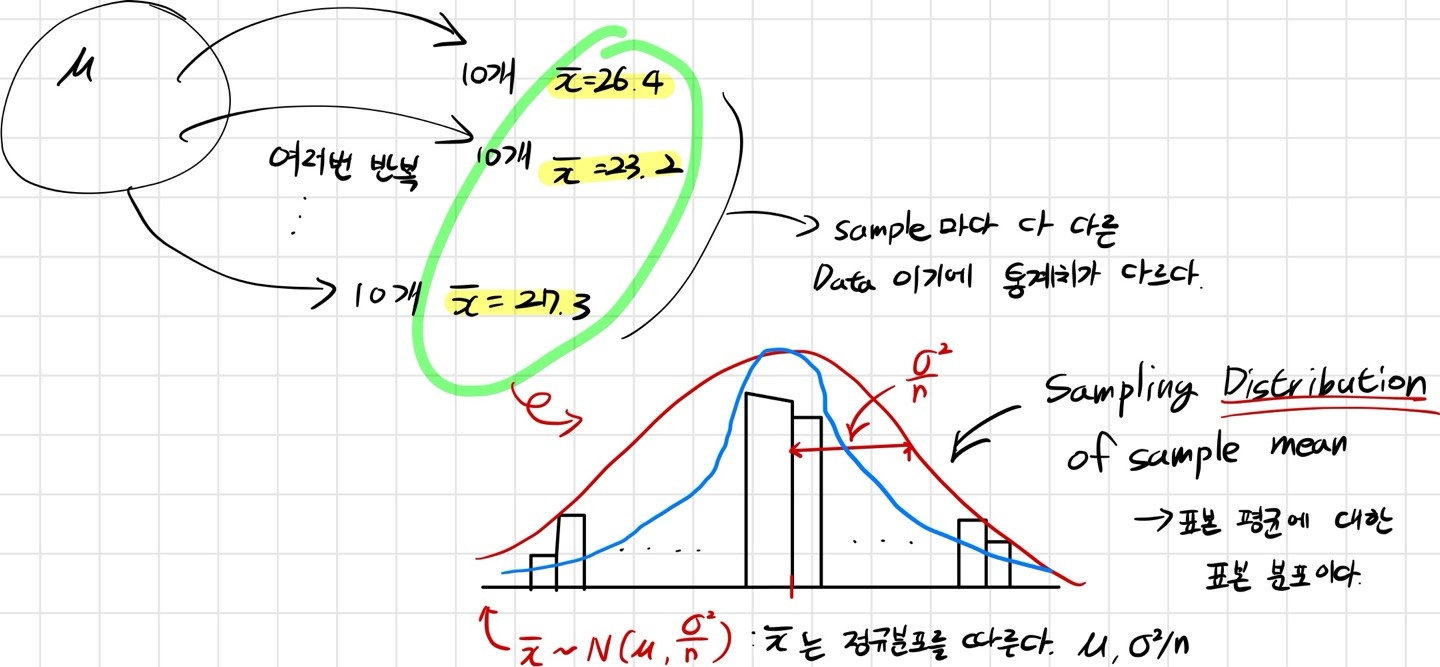
해당 그림은 표본 평균에 대한 표본 분포입니다. 이렇게 샘플링을 많이 할 수록 정규분포를 따르게 됩니다.
그리고 샘플링의 횟수가 많아질 수록 표본 평균의 변동성(흩어짐 정도)이 줄어들어 표본 평균의 분산의 값이 작아지게 됩니다.( = 표본들이 평균에 밀집해 있다! 또는 추정치가 안정적이고 신뢰성이 있다.)
즉, 샘플이 많을수록 그래프는 좁아지게 됩니다!
모평균과 표본 평균의 분산 구하는 공식도 살펴 보겠습니다.
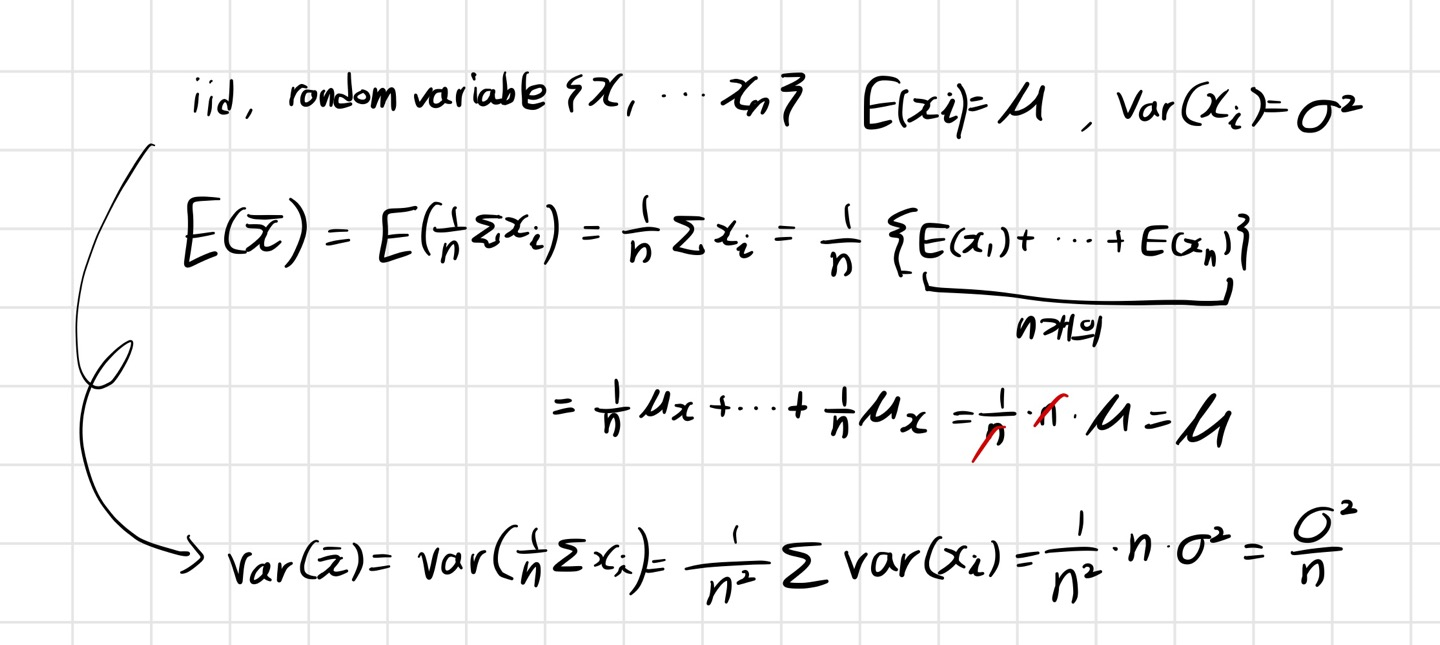
이렇게 나눠질 것은 나눠지고 하다보면 표본평균과 표본 표준편차를 사용하여 표본 평균의 분산과 모평균의 값을 구할 수 있습니다.
해당 내용은 Data Scientist 이지영님의 영상을 보고 공부한 내용입니다.
이상입니다.
'Data Analyst > 기초 통계' 카테고리의 다른 글
| [기초 통계] 1종 오류, 2종 오류 (0) | 2024.10.30 |
|---|---|
| [기초 통계]가설 검정(Hypothesis Test) (0) | 2024.10.29 |
| [기초 통계] 정규분포, 비대칭도, 첨도 (0) | 2024.10.23 |
| [기초 통계] 정규분포, 중심 극한 정리 (0) | 2024.10.22 |
| [기초 통계] Positive & Negative Skew(Mean vs Median) (1) | 2024.10.21 |
1. 모집단(Population)
연구대상이라고도 한다. 하지만 모집단은 우리가 알아낼 수 없습니다.
SRS(Simple Random Sampling) : 모집단 전체를 조사할 수 없기 때문에 사용합니다.
2. 표본(Sample)
모집단을 알아낼 수 없기에 모집단과 비슷한 집단의 데이터들을 뽑아낸 것을 우리는 표본이라합니다.
표본에서 알아낸 통계치를 x_bar(표본 평균), S(표본 표준편차) 이용하여 모수를 추정합니다.
모수: 모집단에서 얻을 수 있는 평균(u)과 표준편차(seta) 등의 통계치를 말합니다.
3. 표본 분포
표본을 뽑으면 그 값이 모집단의 모수와 얼마나 가까운지 모르기에 여러번의 sampling을 통해 각각의 통계치를 분포로 나타낸 것이다.

해당 그림은 표본 평균에 대한 표본 분포입니다. 이렇게 샘플링을 많이 할 수록 정규분포를 따르게 됩니다.
그리고 샘플링의 횟수가 많아질 수록 표본 평균의 변동성(흩어짐 정도)이 줄어들어 표본 평균의 분산의 값이 작아지게 됩니다.( = 표본들이 평균에 밀집해 있다! 또는 추정치가 안정적이고 신뢰성이 있다.)
즉, 샘플이 많을수록 그래프는 좁아지게 됩니다!
모평균과 표본 평균의 분산 구하는 공식도 살펴 보겠습니다.
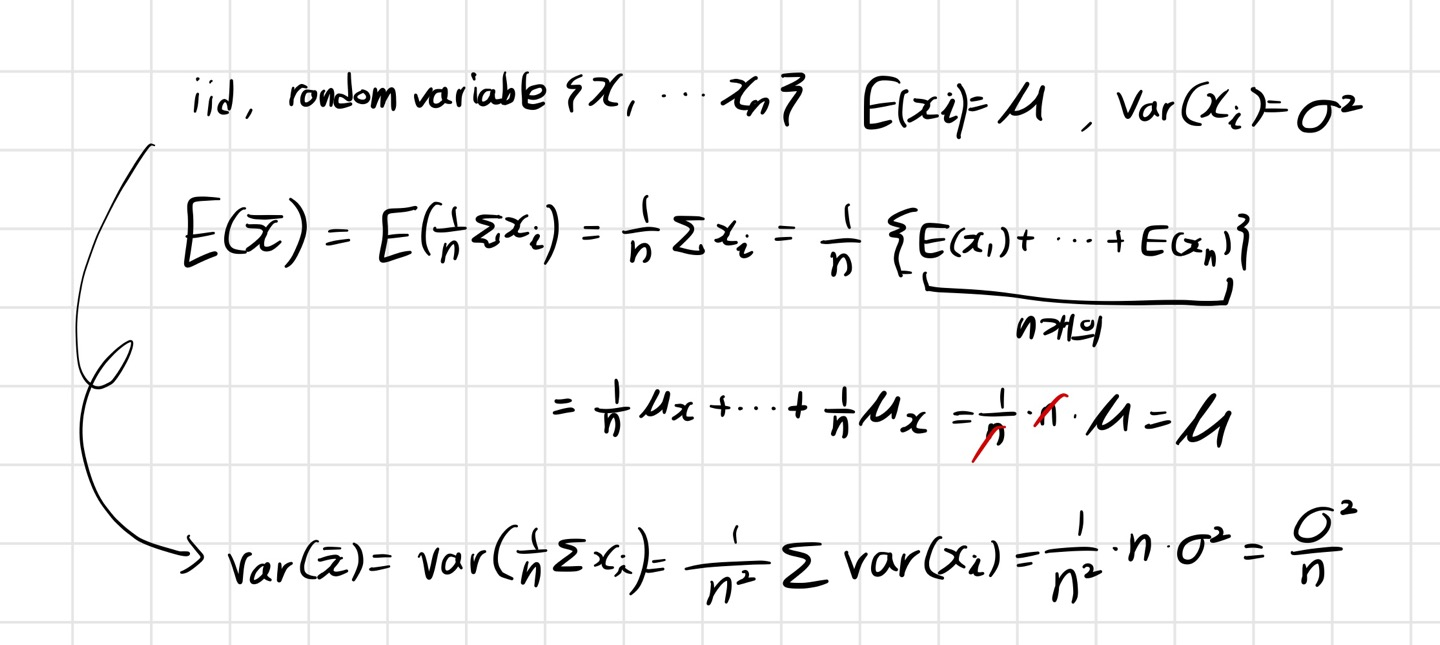
이렇게 나눠질 것은 나눠지고 하다보면 표본평균과 표본 표준편차를 사용하여 표본 평균의 분산과 모평균의 값을 구할 수 있습니다.
해당 내용은 Data Scientist 이지영님의 영상을 보고 공부한 내용입니다.
이상입니다.
'Data Analyst > 기초 통계' 카테고리의 다른 글
| [기초 통계] 1종 오류, 2종 오류 (0) | 2024.10.30 |
|---|---|
| [기초 통계]가설 검정(Hypothesis Test) (0) | 2024.10.29 |
| [기초 통계] 정규분포, 비대칭도, 첨도 (0) | 2024.10.23 |
| [기초 통계] 정규분포, 중심 극한 정리 (0) | 2024.10.22 |
| [기초 통계] Positive & Negative Skew(Mean vs Median) (1) | 2024.10.21 |