1. 가설 이란?
모수에 대해서 얼마나 된다는 주장 이 것을 가설이라 합니다.
2. 가설 검정
A, B에 대해서 Sample 데이터를 얻어서 이 가설이 어떻게 합당한지 어느 상황에 있는지 살펴보고, 이 상황에 따라서 가설을 선택하는 것이 가설검정입니다.
또는, 모집단에 대해서 어떤 모수를 잘 설명할 수 있는 가설입니다.
모수(parameter) : 모집단에 대한 성격을 가진 고정된 수입니다.(하지만, 우리는 알 수가 없는 수입니다.)
즉, 가설은 모집단의 수를 추정하는 것이기 때문에 "H0 : x_bar = 0"이라 하면 틀린 것이다 왜냐하면 x_bar는 표본 평균이므로 모집단 수가 아니기 때문이다.
그래서 "H0 : seta = 0"이라 써야 맞는 것이다.
그리고 가설을 설정할 때 두 개가 겹치는 내용이 있어서는 안된다!!
3. 귀무가설 & 대립가설
1. 귀무가설 정의
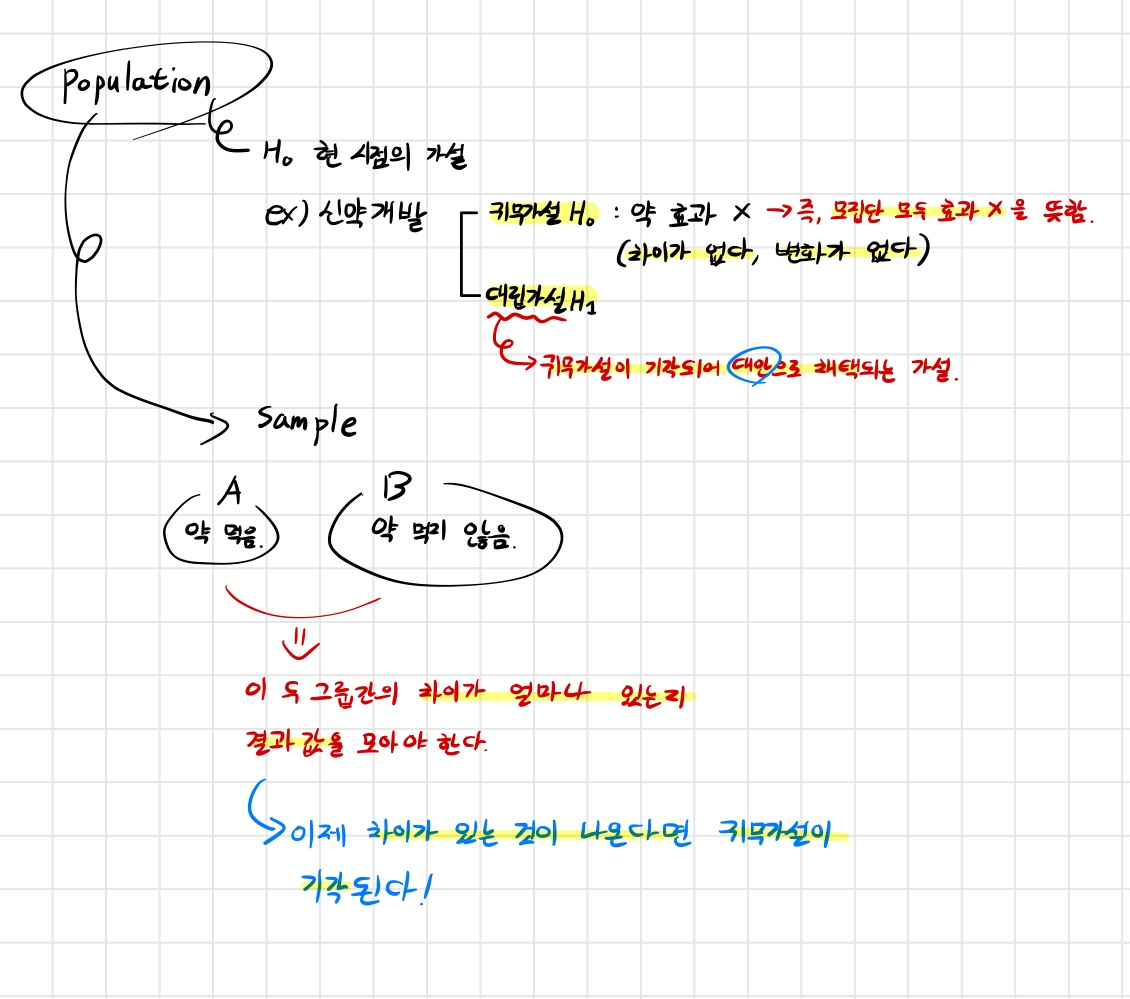
현 시점의 가설을 말합니다.
신약 개발로 예시를 들겠습니다.
귀무가설 : 약 효과가 없다. -> 즉, 모집단 모두 효과가 없는 것을 뜻합니다.(차이가 없다, 변화가 없다.)
2. 대립가설 정의
귀무가설이 기각 되어 대안으로 채택되는 가설을 말합니다..
대립가설 : 약 효과가 있다. -> 즉, 모집단 모두 효과가 있을 것을 뜻합니다.
즉, Sample 값들에서 약을 먹은 그룹 A와 약을 먹지 않은 그룹 B 간의 차이가 얼마나 있는지 결과 값을 모아야 합니다.
여기서 차이가 있는 결과 값이 나온다면 귀무가설은 기각됩니다!!
4. Reject 귀무가설 & Do not reject 귀무가설
Sample에서 Test한 값에 따라서 얼마나 증거가 충분히 모였는지 아닌지에 따라서 두가지로 나뉩니다.
1. Reject H0 : 충분한 증거가 모여 귀무가설 기각한 경우 -> H1(대립가설) 채택!!
2. Do not reject H0 : 충분한 증거를 모으지 못했다. -> H0(귀무가설) 채택!!
반드시 알아야 할 것!!(중요)
"귀무가설을 기각한 것일 뿐, 대립가설이 무조건 맞다는 의미는 아니다" 라는 것을 명심할 것!!
그래서 "Accept H1"은 사용할 수 없는 말이다!!
해당 내용은 Data Scientist 이지영님의 영상을 보고 공부한 내용입니다.
이상입니다.
'Data Analyst > 기초 통계' 카테고리의 다른 글
| [기초 통계] 조건부 확률 (0) | 2024.10.31 |
|---|---|
| [기초 통계] 1종 오류, 2종 오류 (0) | 2024.10.30 |
| [기초 통계] 표본 분포 이해하기 (0) | 2024.10.28 |
| [기초 통계] 정규분포, 비대칭도, 첨도 (0) | 2024.10.23 |
| [기초 통계] 정규분포, 중심 극한 정리 (0) | 2024.10.22 |
1. 가설 이란?
모수에 대해서 얼마나 된다는 주장 이 것을 가설이라 합니다.
2. 가설 검정
A, B에 대해서 Sample 데이터를 얻어서 이 가설이 어떻게 합당한지 어느 상황에 있는지 살펴보고, 이 상황에 따라서 가설을 선택하는 것이 가설검정입니다.
또는, 모집단에 대해서 어떤 모수를 잘 설명할 수 있는 가설입니다.
모수(parameter) : 모집단에 대한 성격을 가진 고정된 수입니다.(하지만, 우리는 알 수가 없는 수입니다.)
즉, 가설은 모집단의 수를 추정하는 것이기 때문에 "H0 : x_bar = 0"이라 하면 틀린 것이다 왜냐하면 x_bar는 표본 평균이므로 모집단 수가 아니기 때문이다.
그래서 "H0 : seta = 0"이라 써야 맞는 것이다.
그리고 가설을 설정할 때 두 개가 겹치는 내용이 있어서는 안된다!!
3. 귀무가설 & 대립가설
1. 귀무가설 정의
현 시점의 가설을 말합니다.
신약 개발로 예시를 들겠습니다.
귀무가설 : 약 효과가 없다. -> 즉, 모집단 모두 효과가 없는 것을 뜻합니다.(차이가 없다, 변화가 없다.)
2. 대립가설 정의
귀무가설이 기각 되어 대안으로 채택되는 가설을 말합니다..
대립가설 : 약 효과가 있다. -> 즉, 모집단 모두 효과가 있을 것을 뜻합니다.
즉, Sample 값들에서 약을 먹은 그룹 A와 약을 먹지 않은 그룹 B 간의 차이가 얼마나 있는지 결과 값을 모아야 합니다.
여기서 차이가 있는 결과 값이 나온다면 귀무가설은 기각됩니다!!

4. Reject 귀무가설 & Do not reject 귀무가설
Sample에서 Test한 값에 따라서 얼마나 증거가 충분히 모였는지 아닌지에 따라서 두가지로 나뉩니다.
1. Reject H0 : 충분한 증거가 모여 귀무가설 기각한 경우 -> H1(대립가설) 채택!!
2. Do not reject H0 : 충분한 증거를 모으지 못했다. -> H0(귀무가설) 채택!!
반드시 알아야 할 것!!(중요)
"귀무가설을 기각한 것일 뿐, 대립가설이 무조건 맞다는 의미는 아니다" 라는 것을 명심할 것!!
그래서 "Accept H1"은 사용할 수 없는 말이다!!
해당 내용은 Data Scientist 이지영님의 영상을 보고 공부한 내용입니다.
이상입니다.
'Data Analyst > 기초 통계' 카테고리의 다른 글
| [기초 통계] 조건부 확률 (0) | 2024.10.31 |
|---|---|
| [기초 통계] 1종 오류, 2종 오류 (0) | 2024.10.30 |
| [기초 통계] 표본 분포 이해하기 (0) | 2024.10.28 |
| [기초 통계] 정규분포, 비대칭도, 첨도 (0) | 2024.10.23 |
| [기초 통계] 정규분포, 중심 극한 정리 (0) | 2024.10.22 |