1. Skewness(비대칭도)
해당 수치를 보고 왼쪽 또는 오른쪽으로 꼬리가 긴 모양을 가졌을 거라는 판단을 할 수 있습니다.
앞서 배운 Positive & Negative Skew에서 말했던 그래프를 떠올리시면 됩니다.
2. Kurtosis(첨도)
Outlier 정도 입니다. 즉, 얼마나 Outlier를 가지고 있는지에 대한 값입니다.
만약 Kurtosis의 값이 매우 크다면 Outlier 값이 좀 있다라는 것을 알 수 있습니다.
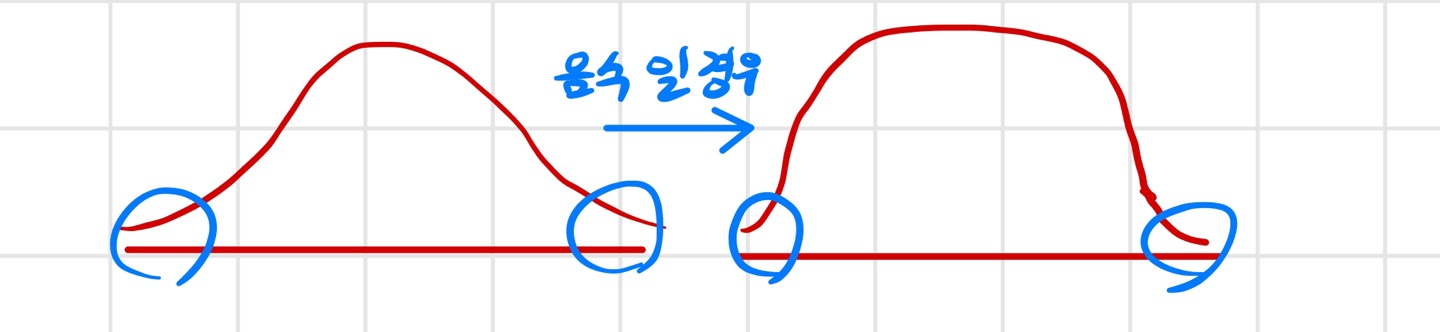
그럼 Kurtosis의 값이 음수라면 위의 그림과 같이 정규분포가 가지는 끝에 나오는 값보다 더 적은 것을 의미합니다.
즉, 끝 값이 정규 분포 보다 더 적게 나오는 것입니다.
3. 예시 설명
A지역과 B지역이 있다고 가정해보겠습니다. 그리고 Skewness와 Kurtosis 값을 정보로 주었습니다.
A지역의 Skewness는 1.21, Kurtosis는 1.8 입니다.
B지역의 Skewness는 0.14, Kurtosis는 5.9 입니다.
해당 내용을 정리하면 A지역의 Skewness는 평균과 중간의 값이 차이가 좀 있는 것으로 추정되며 Kurtosis는 B지역보다 적은 것을 보아 Outlier가 좀 더 적은 것을 의미합니다.
B지역의 Skewness를 보아 평균값과 중간값이 비슷한 것으로 추정됩니다. 그리고 Kurtosis를 보면 Outlier가 좀 있는 것으로 보입니다.
4. 추가 내용
데이터를 어떻게 이해할 수 있을까?!
즉, 저희는 수치형 데이터가 있을 경우 해당 수치가 어떻게 분포하고 있는지 알아야 합니다.
이 말은 어떤 모양으로 그래프가 이루어져 있는지를 확인해야 한다는 것입니다. 그리고 나서 위에서 배운 내용을 적용하여 그래프를 해석해보는 것입니다.
0에 가까운 Skewness, kurtosis 값을 가졌다고 해서 정규 분포라 할 수 있을 것인가?
정답 : 아니다!!
이유는 Skewness, Kurtosis 값은 data가 얼마나 끝쪽에 데이터가 있는지 혹은 Outlier가 있는지 파악하는데 쓰입니다. 그러므로 Skewness, Kurtosis가 0이라 해서 정규 분포가 된다고는 말하기 어렵습니다!!
해당 내용은 Data Scientist 이지영님의 영상을 보고 공부한 내용입니다.
이상입니다.
'Data Analyst > 기초 통계' 카테고리의 다른 글
| [기초 통계]가설 검정(Hypothesis Test) (0) | 2024.10.29 |
|---|---|
| [기초 통계] 표본 분포 이해하기 (0) | 2024.10.28 |
| [기초 통계] 정규분포, 중심 극한 정리 (0) | 2024.10.22 |
| [기초 통계] Positive & Negative Skew(Mean vs Median) (1) | 2024.10.21 |
| [기초 통계] 이산 데이터 VS 연속성 데이터 (2) | 2024.10.16 |
1. Skewness(비대칭도)
해당 수치를 보고 왼쪽 또는 오른쪽으로 꼬리가 긴 모양을 가졌을 거라는 판단을 할 수 있습니다.
앞서 배운 Positive & Negative Skew에서 말했던 그래프를 떠올리시면 됩니다.
2. Kurtosis(첨도)
Outlier 정도 입니다. 즉, 얼마나 Outlier를 가지고 있는지에 대한 값입니다.
만약 Kurtosis의 값이 매우 크다면 Outlier 값이 좀 있다라는 것을 알 수 있습니다.

그럼 Kurtosis의 값이 음수라면 위의 그림과 같이 정규분포가 가지는 끝에 나오는 값보다 더 적은 것을 의미합니다.
즉, 끝 값이 정규 분포 보다 더 적게 나오는 것입니다.
3. 예시 설명
A지역과 B지역이 있다고 가정해보겠습니다. 그리고 Skewness와 Kurtosis 값을 정보로 주었습니다.
A지역의 Skewness는 1.21, Kurtosis는 1.8 입니다.
B지역의 Skewness는 0.14, Kurtosis는 5.9 입니다.
해당 내용을 정리하면 A지역의 Skewness는 평균과 중간의 값이 차이가 좀 있는 것으로 추정되며 Kurtosis는 B지역보다 적은 것을 보아 Outlier가 좀 더 적은 것을 의미합니다.
B지역의 Skewness를 보아 평균값과 중간값이 비슷한 것으로 추정됩니다. 그리고 Kurtosis를 보면 Outlier가 좀 있는 것으로 보입니다.
4. 추가 내용
데이터를 어떻게 이해할 수 있을까?!
즉, 저희는 수치형 데이터가 있을 경우 해당 수치가 어떻게 분포하고 있는지 알아야 합니다.
이 말은 어떤 모양으로 그래프가 이루어져 있는지를 확인해야 한다는 것입니다. 그리고 나서 위에서 배운 내용을 적용하여 그래프를 해석해보는 것입니다.
0에 가까운 Skewness, kurtosis 값을 가졌다고 해서 정규 분포라 할 수 있을 것인가?
정답 : 아니다!!
이유는 Skewness, Kurtosis 값은 data가 얼마나 끝쪽에 데이터가 있는지 혹은 Outlier가 있는지 파악하는데 쓰입니다. 그러므로 Skewness, Kurtosis가 0이라 해서 정규 분포가 된다고는 말하기 어렵습니다!!
해당 내용은 Data Scientist 이지영님의 영상을 보고 공부한 내용입니다.
이상입니다.
'Data Analyst > 기초 통계' 카테고리의 다른 글
| [기초 통계]가설 검정(Hypothesis Test) (0) | 2024.10.29 |
|---|---|
| [기초 통계] 표본 분포 이해하기 (0) | 2024.10.28 |
| [기초 통계] 정규분포, 중심 극한 정리 (0) | 2024.10.22 |
| [기초 통계] Positive & Negative Skew(Mean vs Median) (1) | 2024.10.21 |
| [기초 통계] 이산 데이터 VS 연속성 데이터 (2) | 2024.10.16 |